Dataset Viewer
id
stringlengths 1
4
| question
stringlengths 38
1.5k
| options
sequencelengths 0
5
| image
stringlengths 12
15
| decoded_image
imagewidth (px) 96
2.52k
| answer
stringlengths 1
24
| solution
stringlengths 0
2.39k
⌀ | level
int64 1
5
| subject
stringclasses 15
values |
|---|---|---|---|---|---|---|---|---|
1831 | Two squares with side 1 have a common vertex, and the edge of one of them lies along the diagonal of the other. What is the area of the overlap between the squares? <image1> | [
"$\\sqrt{2}-1$",
"$\\frac{\\sqrt{2}}{2}$",
"$\\frac{\\sqrt{2}+1}{2}$",
"$\\sqrt{2}+1$",
"$\\sqrt{3}-\\sqrt{2}$"
] | images/1831.jpg | A | 4 | transformation geometry |
||
1689 | A rectangular strip of paper of dimensions $4 \times 13$ is folded as shown in the diagram. Two rectangle s are formed with areas $P$ and $Q$ where $P=2 Q$. What is the value of $x$ ? <image1> | [] | images/1689.jpg | 6 | Let the height of the rectangle $Q$ be $y$. Since the original $4 \times 13$ rectangle has been folded to form the second shape, both the width of the rectangle with area $Q$ and the height of the rectangle with area $P$ are 4 . Considering the base of the rectangle before and after folding gives the equation $x+4+y=13$ and hence $x+y=9$. Since the two rectangles both have one side of length 4, the condition $P=2 Q$ implies that $x=2 y$ and so $y=3$ and $x=6$. | 3 | transformation geometry |
|
1261 | $15 \%$ of a round cake is cut as shown in the figure. How many degrees is the angle denoted by the question mark?
<image1> | [
"$30^{\\circ}$",
"$45^{\\circ}$",
"$54^{\\circ}$",
"$15^{\\circ}$",
"$20^{\\circ}$"
] | images/1261.jpg | C | null | 2 | metric geometry - angle |
|
2976 | In the diagram, points $X$, $Y$ and $Z$ are on the sides of $\triangle UVW$, as shown. Line segments $UY$, $VZ$ and $WX$ intersect at $P$. Point $Y$ is on $VW$ such that $VY:YW=4:3$. If $\triangle PYW$ has an area of 30 and $\triangle PZW$ has an area of 35, determine the area of $\triangle UXP$. <image1> | [] | images/2976.jpg | 84 | Recall that if two triangles have their bases along the same straight line and they share a common vertex that is not on this line, then the ratio of their areas is equal to the ratio of the lengths of their bases. We will use this fact extensively throughout the proof.
Let the area of $\triangle PYV$, $\triangle PZU$, $\triangle UXP$, and $\triangle XVP$, be $a$, $b$, $c$, and $d$, respectively. [asy]
size(6cm);
pair v = (0, 0); pair w = (10, 0); pair u = (3.5, 7);
pair y = 4 * w / 7;
pair x = 56 * u / 140;
pair p = IP(w--x, u--y);
pair z = IP(v--(10 * p), u--w);
draw(u--v--w--cycle);
draw(u--y);draw(x--w);draw(z--v);
label("$U$", u, N);
label("$X$", x, NW);
label("$P$", p, NE + 0.2 * W);
label("$Z$", z, NE);
label("$V$", v, SW);
label("$Y$", y, S);
label("$W$", w, SE);
label("$a$", centroid(p, v, y), fontsize(10));
label("$b$", centroid(p, z, u), fontsize(10));
label("$c$", centroid(p, u, x), fontsize(10));
label("$d$", centroid(p, x, v), fontsize(10));
label("$30$", centroid(p, y, w) + 0.2 * W, fontsize(10));
label("$35$", centroid(p, z, w), fontsize(10));
[/asy] Since $$\frac{|\triangle PYV|}{|\triangle PYW|}=\frac{VY}{YW}=\frac{4}{3},$$then $$a = |\triangle PYV|=\frac{4}{3}\times |\triangle PYW|=\frac{4}{3}(30)=40.$$Also, $\frac{|\triangle VZW|}{|\triangle VZU|}=\frac{ZW}{ZU}=\frac{|\triangle PZW|}{|\triangle PZU|}$ or $|\triangle VZW|\times |\triangle PZU| = |\triangle PZW| \times |\triangle VZU|$. Thus, $$\frac{|\triangle VZU|}{|\triangle PZU|}=\frac{|\triangle VZW|}{|\triangle PZW|}=\frac{35+30+40}{35}=\frac{105}{35}=\frac{3}{1}.$$Therefore, $\frac{|\triangle VZU|}{|\triangle PZU|}=\frac{3}{1}$, or $\frac{b+c+d}{b}=\frac{3}{1}$ or $b+c+d=3b$ and $c+d=2b$.
Next, $$\frac{|\triangle UVY|}{|\triangle UYW|}=\frac{VY}{YW}=\frac{4}{3},$$so $$\frac{40+c+d}{30+35+b}=\frac{4}{3}.$$Since $c+d=2b$, we have $3(40+2b)=4(65+b)$, so $120+6b=260+4b$, then $2b=140$ and $b=70$.
Next, $$\frac{|\triangle UXW|}{|\triangle XVW|}=\frac{UX}{XV}=\frac{|\triangle UXP|}{|\triangle XVP|},$$or $$\frac{35+b+c}{30+a+d}=\frac{c}{d}.$$Since $b=70$ and $a=40$, $\frac{105+c}{70+d}=\frac{c}{d}$, or $d(105+c)=c(70+d)$. Thus, $105d+cd=70c+cd$ or $105d=70c$, and $\frac{d}{c}=\frac{70}{105}=\frac{2}{3}$ or $d=\frac{2}{3}c$.
Since $c+d=2b=2(70)=140$, we have $$c+d=c+\frac{2}{3}c=\frac{5}{3}c=140,$$or $c=\frac{3}{5}(140)=84$. Therefore, the area of $\triangle UXP$ is $\boxed{84}$. | 4 | metric geometry - area |
|
2788 | Along the route of a bicycle race, $7$ water stations are evenly spaced between the start and finish lines, as shown in the figure below. There are also $2$ repair stations evenly spaced between the start and finish lines. The $3$rd water station is located $2$ miles after the $1$st repair station. How long is the race in miles?
<image1> | [] | images/2788.jpg | 48 | null | 2 | metric geometry - length |
|
1117 | On a pond 16 lilly pads are arranged in a $4 \times 4$ grid as can be seen in the diagram. A frog sits on a lilly pad in one of the corners of the grid (see picture). The frog jumps from one lilly pad to another horizontally or vertically. In doing so he always jumps over at least one lilly pad. He never lands on the same lilly pad twice. What is the maximum number of lilly pads, including the one he is sitting on, on which he can land?
<image1> | [] | images/1117.jpg | 16 | null | 3 | graph theory |
|
964 | All vehicles in the garage can only drive forwards or backwards. The black car wants to leave the garage (see diagram). What is the minimum number of grey vehicles that need to move at least a little bit so that this is possible?
<image1> | [] | images/964.jpg | 4 | null | 2 | logic |
|
2692 | Eight points are spaced around at intervals of one unit around a $2 \times 2$ square, as shown. Two of the $8$ points are chosen at random. What is the probability that the two points are one unit apart?
<image1> | [
"$\\frac{1}{4}$",
"$\\frac{2}{7}$",
"$\\frac{4}{11}$",
"$\\frac{1}{2}$",
"$\\frac{4}{7}$"
] | images/2692.jpg | B | null | 2 | combinatorics |
|
912 | 4 equally heavy black pearls, 1 white pearl and a piece of iron weighing $30 \mathrm{~g}$ are placed on a beam balance as shown in the diagram. The beam balance is balanced. How heavy are 6 black and 3 white pearls altogether?
<image1> | [
"$100 \\mathrm{~g}$",
"$99 \\mathrm{~g}$",
"$96 \\mathrm{~g}$",
"$94 \\mathrm{~g}$",
"$90 \\mathrm{~g}$"
] | images/912.jpg | E | null | 2 | algebra |
|
1283 | The area of the shaded shape is equal to $2 \pi$ (see the picture). What is the value of the chord $A B$?
<image1> | [] | images/1283.jpg | 4 | null | 4 | metric geometry - length |
|
1992 | Vumos wants to write the integers 1 to 9 in the nine boxes shown so that the sum of the integers in any three adjacent boxes is a multiple of 3 . In how many ways can he do this? <image1> | [
"$6 \\times 6 \\times 6 \\times 6$",
"$6 \\times 6 \\times 6$",
"$2 \\times 2 \\times 2 \\times 2 \\times 2 \\times 2 \\times 2 \\times 2 \\times 2$",
"$6 \\times 5 \\times 4 \\times 3 \\times 2 \\times 1$",
"$9 \\times 8 \\times 7 \\times 6 \\times 5 \\times 4 \\times 3 \\times 2 \\times 1$"
] | images/1992.jpg | A | Let $a, b, c, d$ be the numbers in four adjacent boxes. Then both $a+b+c$ and $b+c+d$ must be multiples of 3. Therefore $a-d$ is a multiple of 3. This applies to any entries three apart. So the numbers in the set $\{1,4,7\}$ must be listed three apart; and the same applies to $\{2,5,8\}$ and to $\{3,6,9\}$. This will automatically ensure that the sum of three adjacent numbers is a multiple of 3. There are 3 choices about which of these sets go in the first, fourth and seventh boxes, 2 choices for the next set and 1 for the third. Also there are $3 \times 2 \times 1=6$ choices for which order the numbers in each set are given. That gives the total number of choices as $6 \times 6 \times 6 \times 6$. | 4 | combinatorics |
|
1136 | Within the square $A B C D$ there are four identical rectangles (see diagram). The perimeter of each rectangle is $16 \mathrm{~cm}$. What is the perimeter of this
square?
<image1>square? | [
"$16 \\mathrm{~cm}$",
"$20 \\mathrm{~cm}$",
"$24 \\mathrm{~cm}$",
"$28 \\mathrm{~cm}$",
"$32 \\mathrm{~cm}$"
] | images/1136.jpg | E | null | 2 | metric geometry - length |
|
193 | Points $M$ and $N$ are given on the sides $A B$ and $B C$ of a rectangle $A B C D$. Then the rectangle is divided into several parts as shown in the picture. The areas of 3 parts are also given in the picture. Find the area of the quadrilateral marked with "?".
<image1> | [] | images/193.jpg | 25 | null | 5 | metric geometry - area |
|
1987 | The figure shows two touching semicircles of radius 1 , with parallel diameters $P Q$ and $R S$. What is the square of the distance $P S$ ? <image1> | [
"$16",
"$8+4 \\sqrt{3}$",
"$12$",
"$9$",
"$5+2 \\sqrt{3}$"
] | images/1987.jpg | B | Let $T$ and $U$ be the centres of the two semicircles and $V, W$ be where the perpendiculars from $U$ and $S$ meet $P Q$. Then $T U$ has length 2, and $U V$ and $S W$ have length 1. Using Pythagoras' theorem $T V$ is $\sqrt{3}$. 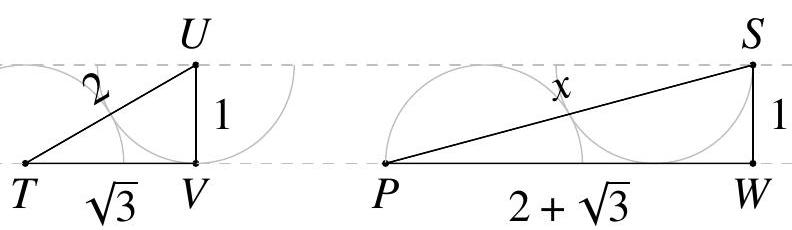 This means that $P W$ is $2+\sqrt{3}$ as it is $T V+2$ radii. So $S P^{2}=(2+\sqrt{3})^{2}+1^{2}$ which is $8+4 \sqrt{3}$. | 4 | metric geometry - length |
|
1358 | The quadrilateral $A B C D$ with side length $4 \mathrm{~cm}$ has the same area as triangle $E C D$. What is the perpendicular distance from point $E$ to the line $g$?
<image1> | [
"$8 \\mathrm{~cm}$",
"$(4+2 \\sqrt{3}) \\mathrm{cm}$",
"$12 \\mathrm{~cm}$",
"$10 \\times \\sqrt{2} \\mathrm{~cm}$",
"It depends on the position of $\\mathrm{E}$."
] | images/1358.jpg | C | null | 4 | metric geometry - length |
|
713 | You have two identical pieces that you can turn around but not upside down. Which picture can you not make with these two pieces?
<image1>
<image2> | [
"A",
"B",
"C",
"D",
"E"
] | images/713.jpg | D | null | 2 | combinatorial geometry |
|
558 | A card has a diagram printed on one side and the other side is plain white. The card is first flipped over to the left and then upwards (see diagram). Which picture do you get this way?
<image1>
<image2> | [
"A",
"B",
"C",
"D",
"E"
] | images/558.jpg | A | null | 1 | transformation geometry |
|
48 | Michael has two building blocks. Each building block is made up of two cubes glued together. Which figure can he not make using the blocks?
<image1>
<image2> | [
"A",
"B",
"C",
"D",
"E"
] | images/48.jpg | B | null | 1 | combinatorial geometry |
|
249 | In the diagram we see a rose bed. White roses are growing in the squares that are equally big, red ones are in the big square and yellow ones in the right-angled triangle. The bed has width and height $16 \mathrm{~m}$. How big is the area of the bed?
<image1> | [
"$114 \\mathrm{~m}^{2}$",
"$130 \\mathrm{~m}^{2}$",
"$144 \\mathrm{~m}^{2}$",
"$160 \\mathrm{~m}^{2}$",
"$186 \\mathrm{~m}^{2}$"
] | images/249.jpg | C | null | 5 | metric geometry - area |
|
2504 | What is the area of polygon $ ABCDEF$?
<image1> | [] | images/2504.jpg | 46 | null | 3 | metric geometry - area |
|
1209 | Each of the five vases shown has the same height and each has a volume of 1 litre. Half a litre of water is poured into each vase. In which vase would the level of the water be the highest?
<image1> | [
"A",
"B",
"C",
"D",
"E"
] | images/1209.jpg | A | null | 4 | solid geometry |
|
294 | On the number wall shown the number on each tile is equal to the sum of the numbers on the two tiles directly below it. Which number is on the tile marked with "?"?
<image1> | [] | images/294.jpg | 16 | null | 5 | algebra |
|
210 | We take three points from the grid so that they were collinear. How many possibilities do we have?
<image1> | [] | images/210.jpg | 20 | null | 5 | combinatorics |
|
1119 | The word KANGAROO is written on the top of my umbrella. Which of the following pictures shows my umbrella?
<image1>
<image2> | [
"A",
"B",
"C",
"D",
"E"
] | images/1119.jpg | E | null | 4 | descriptive geometry |
|
397 | In the picture the distance $KM=10, LN=15, KN=22$. Find the distance $LM$.
<image1> | [] | images/397.jpg | 3 | null | 3 | metric geometry - length |
|
2213 | In the figure below, $3$ of the $6$ disks are to be painted blue, $2$ are to be painted red, and $1$ is to be painted green. Two paintings that can be obtained from one another by a rotation or a reflection of the entire figure are considered the same. How many different paintings are possible?
<image1> | [] | images/2213.jpg | 12 | null | 4 | combinatorics |
|
2289 | In this diagram, not drawn to scale, figures $\text{I}$ and $\text{III}$ are equilateral triangular regions with respective areas of $32\sqrt{3}$ and $8\sqrt{3}$ square inches. Figure $\text{II}$ is a square region with area $32$ sq. in. Let the length of segment $AD$ be decreased by $12\frac{1}{2} \%$ of itself, while the lengths of $AB$ and $CD$ remain unchanged. The percent decrease in the area of the square is:
<image1> | [
"$12\\frac{1}{2}$",
"$25$",
"$50$",
"$75$",
"$87\\frac{1}{2}$"
] | images/2289.jpg | D | null | 5 | metric geometry - area |
|
2218 | In the figure below, $N$ congruent semicircles lie on the diameter of a large semicircle, with their diameters covering the diameter of the large semicircle with no overlap. Let $A$ be the combined area of the small semicircles and $B$ be the area of the region inside the large semicircle but outside the semicircles. The ratio $A:B$ is $1:18$. What is $N$?
<image1> | [] | images/2218.jpg | 19 | null | 4 | metric geometry - area |
|
1615 | Janet enters all the digits from 1 to 9 in the cells of a $3 \times 3$ table, so that each cell contains one digit. She has already entered 1,2,3 and 4, as shown. Two numbers are considered to be 'neighbours' if their cells share an edge. After entering all the numbers, she notices that the sum of the neighbours of 9 is 15 . What is the sum of the neighbours of 8 ? <image1> | [] | images/1615.jpg | 27 | The sum of the neighbours of 9 is 15 . If 9 were to be placed in the central cell, its neighbours would be $5,6,7$ and 8 with sum 26 so 9 must be placed in one of the cells on the perimeter of the table. So the neighbours of 9 will be the numbers in the middle cell and the two corner cells which are in either the same row or the same column of the table. The largest sum of two such corner cells is $3+4=7$ so, for the sum of the neighbours of 9 to be 15, the number in the middle cell cannot be smaller than 8 . However, the middle square cannot be larger than 8 since we already know 9 is in a perimeter cell. Therefore the number in the middle cell is 8 and its neighbours are 5, 6, 7 and 9 with sum 27. | 4 | logic |
|
2075 | Equilateral triangle $ T$ is inscribed in circle $ A$, which has radius $ 10$. Circle $ B$ with radius $ 3$ is internally tangent to circle $ A$ at one vertex of $ T$. Circles $ C$ and $ D$, both with radius $ 2$, are internally tangent to circle $ A$ at the other two vertices of $ T$. Circles $ B$, $ C$, and $ D$ are all externally tangent to circle $ E$, which has radius $ \frac{m}{n}$, where $ m$ and $ n$ are relatively prime positive integers. Find $ m + n$.
<image1> | [] | images/2075.jpg | 32 | null | 5 | metric geometry - length |
|
2508 | <image1>
In a magic triangle, each of the six whole numbers $ 10-15$ is placed in one of the circles so that the sum, $ S$, of the three numbers on each side of the triangle is the same. The largest possible value for $ S$ is | [] | images/2508.jpg | 39 | null | 4 | algebra |
|
1218 | A triangular pyramid is built with 20 cannon balls, as shown. Each cannon ball is labelled with one of $A, B, C, D$ or $E$. There are 4 cannon balls with each type of label. The picture shows the labels on the cannon balls on 3 of the faces of the pyramid. What is the label on the hidden cannon ball in the middle of the fourth face?
<image1>
<image2> | [
"A",
"B",
"C",
"D",
"E"
] | images/1218.jpg | D | null | 4 | solid geometry |
|
2525 | The shaded region formed by the two intersecting perpendicular rectangles, in square units, is
<image1> | [
"$23$",
"$38$",
"$44$",
"$46$",
"$\\text{unable to be determined from the information given}$"
] | images/2525.jpg | C | null | 3 | metric geometry - area |
|
2551 | Each spinner is divided into $3$ equal parts. The results obtained from spinning the two spinners are multiplied. What is the probability that this product is an even number?
<image1> | [
"$\\frac{1}{3}$",
"$\\frac{1}{2}$",
"$\\frac{2}{3}$",
"$\\frac{7}{9}$",
"$1$"
] | images/2551.jpg | D | null | 2 | combinatorics |
|
942 | When the 5 pieces <image1> are fitted together correctly, the result is a rectangle with a calculation written on it. What is the answer to this calculation? | [] | images/942.jpg | 32 | null | 3 | arithmetic |
|
2516 | The area of the rectangular region is
<image1> | [
"$\\text{.088 m}^2$",
"$\\text{.62 m}^2$",
"$\\text{.88 m}^2$",
"$\\text{1.24 m}^2$",
"$\\text{4.22 m}^2$"
] | images/2516.jpg | A | null | 3 | metric geometry - area |
|
192 | The lengths of the sides of triangle $X Y Z$ are $X Z=\sqrt{55}$, $X Y=8, Y Z=9$. Find the length of the diagonal $X A$ of the rectangular parallelepiped in the figure.
<image1> | [] | images/192.jpg | 10 | null | 3 | solid geometry |
|
251 | The clock shown has a rectangular clock face, the hands however move as usual in a constant circular pattern. How big is the distance $x$ of the digits 1 and 2 (in $\mathrm{cm}$ ), if the distance between the numbers 8 and 10 is given as $12 \mathrm{~cm}$?
<image1> | [
"$3 \\sqrt{3}$",
"$2 \\sqrt{3}$",
"$4 \\sqrt{3}$",
"$2+\\sqrt{3}$",
"$12-3 \\sqrt{3}$"
] | images/251.jpg | C | null | 5 | metric geometry - length |
|
2132 | In the figure, $ \angle EAB$ and $ \angle ABC$ are right angles. $ AB = 4, BC = 6, AE = 8$, and $ \overline{AC}$ and $ \overline{BE}$ intersect at $ D$. What is the difference between the areas of $ \triangle ADE$ and $ \triangle BDC$?
<image1> | [] | images/2132.jpg | 4 | null | 4 | metric geometry - area |
|
2952 | The trapezoid shown has a height of length $12\text{ cm},$ a base of length $16\text{ cm},$ and an area of $162\text{ cm}^2.$ What is the perimeter of the trapezoid? <image1> | [] | images/2952.jpg | 52 | We first label the trapezoid $ABCD$ as shown in the diagram below. Since $AD$ is the height of the trapezoid, then $AB$ and $DC$ are parallel. The area of the trapezoid is \begin{align*}
\frac{AD}{2}\times(AB+DC)&=\frac{12}{2}\times(AB+16) \\
&=6\times(AB+16).
\end{align*} Since the area of the trapezoid is $162,$ we have $6\times(AB+16)=162$ so that $$AB+16=\frac{162}{6}.$$ Solving for $AB$, we obtain $AB=11.$
Construct a perpendicular from $B$ to $E$ on $DC.$ Since $AB$ and $DE$ are parallel, and both $AD$ and $BE$ are perpendicular to $DE,$ we know that $ABED$ is a rectangle. Thus, $DE=AB=11,$ $BE=AD=12,$ and \begin{align*}
EC&=DC-DE \\
&=16-11 \\
&=5.
\end{align*} Since $\angle BEC=90^{\circ},$ we know that $\triangle BEC$ is a right triangle. Thus by the Pythagorean Theorem, \begin{align*}
BC^2&=BE^2+EC^2 \\
&= 12^2+5^2 \\
&= 169
\end{align*} so that $BC=13$ (since $BC>0$).
The perimeter of the trapezoid is $$AB+BC+CD+DA=11+13+16+12=\boxed{52}\text{ cm}.$$ [asy]
draw((0,0)--(0,12)--(11,12)--(16,0)--cycle);
draw((11,0)--(11,12),dashed);
draw((11.7,0)--(11.7,.7)--(11,.7));
label("$A$",(0,12),NW);
label("$B$",(11,12),NE);
label("$C$",(16,0),SE);
label("$E$",(11,0),S);
label("$D$",(0,0),SW);
label("12 cm",(-1,6),W);
label("16 cm",(8,-1),S);
[/asy] | 1 | metric geometry - length |
|
2358 | In $ \triangle ABC$, we have $ \angle C = 3 \angle A$, $ a = 27$, and $ c = 48$. What is $ b$?
<image1> | [
"$33$",
"$35$",
"$37$",
"$39$",
"$\\text{not uniquely determined}$"
] | images/2358.jpg | B | null | 5 | metric geometry - length |
|
531 | Which number is hidden behind the square?
<image1> | [] | images/531.jpg | 6 | null | 2 | algebra |
|
2193 | Equilateral $\triangle ABC$ has side length $1$, and squares $ABDE$, $BCHI$, $CAFG$ lie outside the triangle. What is the area of hexagon $DEFGHI$?
<image1> | [
"$\\frac{12+3\\sqrt{3}}4$",
"$\\frac{9}{2}$",
"$3+\\sqrt{3}$",
"$\\frac{6+3\\sqrt{3}}2$",
"$6$"
] | images/2193.jpg | C | null | 4 | metric geometry - area |
|
471 | Maria folds a square piece of paper in such a way that the kangaroos exactly overlap each other. Along how many of the lines shown is this possible?
<image1> | [] | images/471.jpg | 2 | null | 1 | transformation geometry |
|
2819 | Consider constructing a tower of tables of numbers as follows. <image1> <image2> The first table is a one by one array containing the single number $1$.\nThe second table is a two by two array formed underneath the first table and built as followed. For each entry, we look at the terms in the previous table that are directly up and to the left, up and to the right, and down and to the right of the entry, and we fill that entry with the sum of the numbers occurring there. If there happens to be no term at a particular location, it contributes a value of zero to the sum.\n\nThe diagram above shows how we compute the second table from the first.\nThe diagram below shows how to then compute the third table from the second.\n\nFor example, the entry in the middle row and middle column of the third table is equal the sum of the top left entry $1$, the top right entry $0$, and the bottom right entry $1$ from the second table, which is just $2$.\nSimilarly, to compute the bottom rightmost entry in the third table, we look above it to the left and see that the entry in the second table's bottom rightmost entry is $1$. There are no entries from the second table above it and to the right or below it and to the right, so we just take this entry in the third table to be $1$.\nWe continue constructing the tower by making more tables from the previous tables. Find the entry in the third (from the bottom) row of the third (from the left) column of the tenth table in this resulting tower. | [] | images/2819.jpg | 756 | Let $a_{j, k}^{(i)}$ denote the entry in the $j^{\text {th }}$ row and $k^{\text {th }}$ column of the $i^{\text {th }}$ table in the tower, where the row index $j$ starts at zero (for the bottom row), the column index $k$ starts at zero (for the leftmost column), and the index $i$ starts at one.\nTo each table in the tower, we can associate the polynomial\n$$\nf_i(x, y)=\sum_{j=0}^{i-1} \sum_{k=0}^{i-1} a_{j, k}^{(i)} x^j y^k .\n$$\n\nThe recursion we use to build up the $(i+1)^{\text {th }}$ table from the $i^{\text {th }}$ table corresponds to the polynomial recurrence\n$$\nf_{i+1}(x, y)=(1+x+y) \cdot f_i(x, y) .\n$$\n\nSince $f_1(x, y)=1$, it follows that\n$$\nf_i(x, y)=(1+x+y)^{i-1} .\n$$\n\nHence when the problem is asking us to find the entry in the third (from the bottom) row of the third (from the left) column of the tenth table in the tower, it is really asking us to compute the coefficient of $x^2 y^2$ in $f_{10}(x, y)$. There are multiple ways find the answer from this point. If we use the binomial theorem, we can get that the answer is\n$$\n\left(\begin{array}{l}\n4 \\n2\n\end{array}\right)\left(\begin{array}{l}\n9 \\n4\n\end{array}\right)=6 \cdot(9 \cdot 2 \cdot 7)=756\n$$ | 5 | algebra |
|
2414 | Points $A, B$ and $C$ on a circle of radius $r$ are situated so that $AB=AC, AB>r$, and the length of minor arc $BC$ is $r$. If angles are measured in radians, then $AB/BC=$
<image1> | [
"$\\frac{1}{2}\\csc{\\frac{1}{4}}$",
"$2\\cos{\\frac{1}{2}}$",
"$4\\sin{\\frac{1}{2}}$",
"$\\csc{\\frac{1}{2}}$",
"$2\\sec{\\frac{1}{2}}$"
] | images/2414.jpg | A | null | 5 | metric geometry - length |
|
2932 | In the figure below $AB = BC$, $m \angle ABD = 30^{\circ}$, $m \angle C = 50^{\circ}$ and $m \angle CBD = 80^{\circ}$. What is the number of degrees in the measure of angle $A$?
<image1> | [] | images/2932.jpg | 75 | We know two of the angles in $\triangle BCD$: $$m\angle CBD = 80^\circ, ~~m\angle BCD = 50^\circ.$$ Since the sum of angles in a triangle is $180^\circ$, we conclude that $m\angle BDC = 180^\circ - (50^\circ+80^\circ) = 50^\circ$.
Therefore, $\triangle BCD$ is isosceles with equal angles at $C$ and $D$, which implies that the sides opposite those angles ($BD$ and $BC$) are equal.
Since we are given $AB=BC$, we now know that $AB=BD$, which means that $\triangle ABD$ is isosceles with equal angles at $A$ and $D$. Let $x = m\angle A$. Then the sum of angles in $\triangle ABD$ is $180^\circ$, so $$x + x + 30^\circ = 180^\circ.$$ We can solve this equation to get $x = 75^\circ$. So, $m\angle A = \boxed{75^\circ}$. | 1 | metric geometry - angle |
|
176 | How many triangles can be drawn with vertices in the 18 points shown in the figure?
<image1> | [] | images/176.jpg | 711 | null | 5 | combinatorics |
|
179 | A square piece of paper has been cut in three pieces. Two of them are in the picture on the right. What is the third one?
<image1>
<image2> | [
"A",
"B",
"C",
"D",
"E"
] | images/179.jpg | A | null | 5 | combinatorial geometry |
|
2772 | The Math Team designed a logo shaped like a multiplication symbol, shown below on a grid of 1-inch squares. What is the area of the logo in square inches?
<image1> | [] | images/2772.jpg | 10 | null | 4 | combinatorial geometry |
|
1715 | Some mice live in three neighbouring houses. Last night, every mouse left its house and moved to one of the other two houses, always taking the shortest route. The numbers in the diagram show the number of mice per house, yesterday and today. How many mice used the path at the bottom of the diagram? <image1> | [] | images/1715.jpg | 11 | Let the number of mice that travelled from the left-hand house to the right-hand house along the bottom path be $x$ and the number of mice that travelled from the right-hand house to the left-hand house be $y$. Therefore, since every mouse changed house last night, $8-x$ mice travelled from the left-hand house to the top house and $7-y$ mice travelled from the right-hand house to the top house. Hence, since there were then 4 mice in the top house, we have $8-x+7-y=4$ and so $x+y=11$. Therefore the number of mice that travelled along the bottom path in the diagram is 11 . | 3 | counting |
|
666 | Five cars are labelled with the numbers 1 to 5 . They drive in the direction of the arrow.
<image1>
First the last car overtakes the two cars in front of it.
Then the now second to last car overtakes the two in front of it.
In the end the car that is now in the middle overtakes the two in front of it.
In which order do the cars now drive? | [
"$1,2,3,4,5$",
"$2,1,3,5,4$",
"$2,1,5,3,4$",
"$3,1,4,2,5$",
"$4,1,2,5,3$"
] | images/666.jpg | B | null | 2 | combinatorial geometry |
|
2958 | Quadrilateral $QABO$ is constructed as shown. Determine the area of $QABO$. <image1> | [] | images/2958.jpg | 84 | If point $T$ is placed at $(2,0)$, then $T$ is on $OB$ and $AT$ is perpendicular to $OB$. [asy]
size(5cm);defaultpen(fontsize(9));
pair o = (0, 0); pair q = (0, 12); pair b = (12, 0);
pair a = (2, 12); pair t = (2, 0);
draw((-2, 0)--(15, 0), Arrow);
draw((0, -2)--(0, 15), Arrow);
draw(q--a--b);
draw(a--t);
label("$Q(0, 12)$", q, W);
label("$A(2, 12)$", a, NE);
label("$B(12, 0)$", b, S);
label("$O(0, 0)$", o, SW);
label("$x$", (15, 0), E);
label("$y$", (0, 15), N);
label("$T(2, 0)$", t, S + 0.6 * E);
[/asy] Since $QO$ is perpendicular to $OB$, then $QO$ is parallel to $AT$. Both $QA$ and $OT$ are horizontal, so then $QA$ is parallel to $OT$. Therefore, $QATO$ is a rectangle. The area of rectangle $QATO$ is $QA\times QO$ or $(2-0)\times(12-0)=24$.
Since $AT$ is perpendicular to $TB$, we can treat $AT$ as the height of $\triangle ATB$ and $TB$ as the base. The area of $\triangle ATB$ is $$\frac{1}{2}\times TB\times AT = \frac{1}{2}\times(12-2)\times(12-0)=\frac{1}{2}\times10\times12=60.$$The area of $QABO$ is the sum of the areas of rectangle $QATO$ and $\triangle ATB$, or $24+60=\boxed{84}$. | 2 | analytic geometry |
|
1637 | Katie writes a different positive integer on the top face of each of the fourteen cubes in the pyramid shown.
The sum of the nine integers written on the cubes in the bottom layer is 50. The integer written on each of the cubes in the middle and top layers of the pyramid is equal to the sum of the integers on the four cubes
<image1>
underneath it. What is the greatest possible integer that she can write on the top cube? | [] | images/1637.jpg | 118 | Let the integers written on the small cubes in the bottom layer be arranged as shown. \begin{tabular}{|l|l|l|} \hline$a$ & $b$ & $c$ \\ \hline$d$ & $e$ & $f$ \\ \hline$g$ & $h$ & $i$ \\ \hline \end{tabular} Hence, since the integers written on the cubes in the second and third layers are the sum of the integers on the four cubes underneath, the following is written on the cubes in the second layer. $$ \begin{array}{|l|l|} \hline a+b+d+e & b+c+e+f \\ \hline d+e+g+h & e+f+h+i \\ \hline \end{array} $$ Therefore the integer written on the top cube is $$ \begin{aligned} & (a+b+d+e)+(b+c+e+f)+(d+e+g+h)+(e+f+h+i) \\ & \quad=(a+b+c+d+e+f+g+h+i)+(b+d+f+h)+3 e \end{aligned} $$ Since the sum of the integers on the bottom layer is 50 , the integer written on the top cube is equal to $50+(b+d+f+h)+3 e$. To maximise this, we first require $e$ to be as large as possible which will be obtained when the other eight integers are as small as possible. Therefore $e=50-(1+2+3+4+5+6+7+8)=14$. Secondly, $(b+d+f+h)$ should now be made as large as possible and hence $b, d, f$ and $h$ are 5, 6, 7 and 8 in any order. Therefore $(b+d+f+h)=5+6+7+8=26$. Hence the greatest possible integer she can write on the top cube is $50+26+3 \times 14=118$. | 4 | algebra |
|
877 | The numbers $1,2,3,4$ and 5 have to be written into the five fields of this diagram according to the following rules: If one number is below another number, it has to be greater; if one number is to the right of another, it has to be greater. How many ways are there to place the numbers?
<image1> | [] | images/877.jpg | 6 | null | 3 | combinatorics |
|
2000 | Both rows of the following grid have the same sum. What is the value of $*$ ?
<image1> | [] | images/2000.jpg | 950 | \begin{tabular}{|c|c|c|c|c|c|c|c|c|c|c|} \hline 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 1050 \\ \hline 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 & 19 & 20 & $*$ \\ \hline \end{tabular} We observe that in all but the rightmost column the value in the second row is ten larger than the value in the first row. There are 10 such columns. Therefore the sum of the leftmost ten elements of the second row is 100 more than the corresponding sum in the first row. To achieve the same total in each row, * will need to be 100 less than the value above it. Therefore $*=950$. | 1 | arithmetic |
|
1420 | Two concentric circles with radii 1 and 9 form an annulus. $n$ circles without overlap are drawn inside this annulus, where every circle touches both circles of the annulus. (The diagram shows an example for $\mathrm{n}=1$ and the other radii as given.) What is the biggest possible value of $n$?
<image1> | [] | images/1420.jpg | 3 | null | 3 | combinatorial geometry |
|
1360 | The diagram shows a right-angled triangle with side lengths 5,12 and 13. What is the length of the radius of the inscribed semi-circle?
<image1> | [
"$7 / 3$",
"$10 / 3$",
"$12 / 3$",
"$13 / 3$",
"$17 / 3$"
] | images/1360.jpg | B | null | 4 | metric geometry - length |
|
1156 | Mike has 125 small, equally big cubes. He glues some of them together in such a way that one big cube with exactly nine tunnels is created (see diagram). The tunnels go all the way straight through the cube. How many of the 125 cubes is he not using?
<image1> | [] | images/1156.jpg | 39 | null | 4 | solid geometry |
|
1691 | A triangular pyramid is built with 20 cannonballs, as shown. Each cannonball is labelled with one of A, B, C, D or E. There are four cannonballs with each type of label.
<image1>
The diagrams show the labels on the cannonballs on three of the faces of the pyramid. What is the label on the hidden cannonball in the middle of the fourth face? | [
"A",
"B",
"C",
"D",
"E"
] | images/1691.jpg | D | Note that each cannonball on the two non-horizontal edges of each pictured face appears on two of those faces, except the cannonball at the vertex which appears on all three. Hence, when the labels of the cannonballs are counted, these must only be counted once. Careful counting of the cannonballs shown gives four cannonballs labelled $A, B, C$ and $E$ but only three labelled $D$. Hence the cannonball at the centre of the hidden face is labelled $D$. | 4 | solid geometry |
|
71 | Each one of the four keys locks exactly one padlock. Every letter on a padlock stands for exactly one digit. Same letters mean same digits.
Which letters must be written on the fourth padlock?
<image1> | [
"GDA",
"ADG",
"GAD",
"GAG",
"DAD"
] | images/71.jpg | D | null | 3 | logic |
|
2375 | $ABC$ and $A'B'C'$ are equilateral triangles with parallel sides and the same center, as in the figure. The distance between side $BC$ and side $B'C'$ is $\frac{1}{6}$ the altitude of $\triangle ABC$. The ratio of the area of $\triangle A'B'C'$ to the area of $\triangle ABC$ is
<image1> | [
"$\\frac{1}{36}$",
"$\\frac{1}{6}$",
"$\\frac{1}{4}$",
"$\\frac{\\sqrt{3}}{4}$",
"$\\frac{9+8\\sqrt{3}}{36}$"
] | images/2375.jpg | C | null | 5 | metric geometry - area |
|
1030 | What is the sum of the points on the invisible faces of the dice?
<image1> | [] | images/1030.jpg | 27 | null | 4 | solid geometry |
|
2201 | A sphere is inscribed in a truncated right circular cone as shown. The volume of the truncated cone is twice that of the sphere. What is the ratio of the radius of the bottom base of the truncated cone to the radius of the top base of the truncated cone?
<image1> | [
"$\\frac{3}{2}$",
"$\\frac{1+\\sqrt{5}}{2}$",
"$\\sqrt{3}$",
"$2$",
"$\\frac{3+\\sqrt{5}}{2}$"
] | images/2201.jpg | E | null | 2 | solid geometry |
|
721 | A butterfly sat down on my correctly solved exercise: 2005-205=25+<image1>
What number is the butterfly covering? | [] | images/721.jpg | 1775 | null | 2 | algebra |
|
891 | Four equally big squares are partially coloured in black. In which of the four squares is the total area of the black parts biggest?
<image1> | [
"A",
"B",
"C",
"D",
"The total area of the black parts is always equally big."
] | images/891.jpg | E | null | 2 | combinatorial geometry |
|
2272 | In a general triangle $ ADE$ (as shown) lines $ \overline{EB}$ and $ \overline{EC}$ are drawn. Which of the following angle relations is true?
<image1> | [
"$x + z = a + b$",
"$y + z = a + b$",
"$m + x = w + n \\\\$",
"$x + z + n = w + c + m$",
"$x + y + n = a + b + m$"
] | images/2272.jpg | E | null | 4 | metric geometry - angle |
|
2491 | The acronym AMC is shown in the rectangular grid below with grid lines spaced $1$ unit apart. In units, what is the sum of the lengths of the line segments that form the acronym AMC$?$
<image1> | [
"$17$",
"$15 + 2\\sqrt{2}$",
"$13 + 4\\sqrt{2}$",
"$11 + 6\\sqrt{2}$",
"$21$"
] | images/2491.jpg | C | null | 5 | metric geometry - length |
|
2839 | Let $T$ be the answer from the previous part. Rectangle $R$ has length $T$ times its width. $R$ is inscribed in a square $S$ such that the diagonals of $ S$ are parallel to the sides of $R$. What proportion of the area of $S$ is contained within $R$?\n<image1> | [] | images/2839.jpg | $\frac{8}{25}$ | Let the width of rectangle $R$ be $2x.$ Then, the length of rectangle $R$ is $8x.$\n\nIt follows that the side length of square $S$ is$$\sqrt{2}x+4\sqrt{2}x=5\sqrt{2}x,$$so the area of the square is$$50x^2.$$\nHence, the answer is$$\frac{16x^2}{50x^2} = \boxed{\frac{8}{25}}.$$ | 5 | metric geometry - area |
|
69 | Lisa has several sheets of construction paper like this
<image1>
and
<image2>
She wants to make 7 identical crowns:
<image3>
For that she cuts out the necessary parts.
What is the minimum number of sheets of construction paper that she has to cut up? | [] | images/69.jpg | 9 | null | 2 | arithmetic |
|
2846 | A drunkard is randomly walking through a city when he stumbles upon a $2 \times 2$ sliding tile puzzle. The puzzle consists of a $2 \times 2$ grid filled with a blank square, as well as $3$ square tiles, labeled $1$, $2$, and $3$. During each turn you may fill the empty square by sliding one of the adjacent tiles into it. The following image shows the puzzle's correct state, as well as two possible moves you can make. Assuming that the puzzle is initially in an incorrect (but solvable) state, and that the drunkard will make completely random moves to try and solve it, how many moves is he expected to make before he restores the puzzle to its correct state?\n<image1> | [] | images/2846.jpg | 7/3 | Note, we can just move the empty space to one of the spots adjacent to it. We win when the empty space is bottom right. By symmetry, this is only a function of distance. Note, $d(1) = 1/2(1) + 1/2d(2), d(2) = d(1) + 1 \implies d(1) = 1/2 + 1/2d(1) + 1/2 \implies d(1) = 2, d(2) = 3.$ There's a $2/3$ chance we're at $d(1)$ and a $1/3$ chance we're at $d(2).$ So, the expected number of moves is $2/3 \cdot 2 + 1/3\cdot 3 = \fbox{7/3}.$ | 5 | combinatorics |
|
553 | A mouse wants to escape a labyrinth. On her way out she is only allowed to go through each opening once at most. How many different ways can the mouse choose to go to get outside?
<image1> | [] | images/553.jpg | 4 | null | 2 | graph theory |
|
2875 | Let $ ABC$ be a triangle with $ AB = 5$, $ BC = 4$ and $ AC = 3$. Let $ \mathcal P$ and $ \mathcal Q$ be squares inside $ ABC$ with disjoint interiors such that they both have one side lying on $ AB$. Also, the two squares each have an edge lying on a common line perpendicular to $ AB$, and $ \mathcal P$ has one vertex on $ AC$ and $ \mathcal Q$ has one vertex on $ BC$. Determine the minimum value of the sum of the areas of the two squares.\n<image1> | [] | images/2875.jpg | $\boxed{\frac{144}{49}}$ | Label $ A(0,0)$ and $ B(5,0)$ and let the intersection of $ \mathcal P$ and $ AC$ be $ D$ and the intersection of $ \mathcal Q$ and $ BC$ be $ E$. Also let $ \mathcal P$ have length $ p$ and $ \mathcal Q$ have length $ q$.\n\nThe slope of line $ AC$ is $ \tan\angle CAB = \frac{4}{3}$. Then label $ D\left(\frac{3}{4}p, p\right)$. Then label $ E\left(\frac{7}{4}p + q,q\right)$.\n\nThe slope of line $ BC$ is $ \tan \angle CBA = \frac{3}{4}$. Write the equation of line $ BC$ as $ y = - \frac{3}{4}x + \frac{15}{4}$. Then $ q = - \frac{3}{4}\left(\frac{7}{4}p + q\right) + \frac{15}{4}$. Then $ 21p + 28q = 60$. By the Cauchy-Schwarz inequality, $ (p^2 + q^2)(21^2 + 28^2)\ge (21p + 28q)^2 = 60^2$. So $ p^2 + q^2\ge\frac{60^2}{21^2 + 28^2} = \frac{60^2}{35^2} = \frac{12^2}{7^2} = \boxed{\frac{144}{49}}$.\n\nEdit: Equality when $ \frac{p}{21}=\frac{q}{28}$, or $ p=\frac{36}{35}, q=\frac{48}{35}$. | 5 | metric geometry - area |
|
928 | Beatriz has five sisters with ages of 2, 3, 5, 8, 10 and 17. Beatriz writes these ages in the circles of the opposite diagram, so that the sum of the ages in the four corners of the square is equal to the sum of the ages in the four circles aligned horizontally. What is this sum?
<image1> | [] | images/928.jpg | 32 | null | 2 | algebra |
|
2521 | The figure consists of alternating light and dark squares.
<image1>
The number of dark squares exceeds the number of light squares by | [] | images/2521.jpg | 11 | null | 4 | algebra |
|
2338 | In the adjoining figure triangle $ ABC$ is inscribed in a circle. Point $ D$ lies on $ \stackrel{\frown}{AC}$ with $ \stackrel{\frown}{DC} = 30^\circ$, and point $ G$ lies on $ \stackrel{\frown}{BA}$ with $ \stackrel{\frown}{BG}\, > \, \stackrel{\frown}{GA}$. Side $ AB$ and side $ AC$ each have length equal to the length of chord $ DG$, and $ \angle CAB = 30^\circ$. Chord $ DG$ intersects sides $ AC$ and $ AB$ at $ E$ and $ F$, respectively. The ratio of the area of $ \triangle AFE$ to the area of $ \triangle ABC$ is
<image1> | [
"$\\frac{2 - \\sqrt{3}}{3}$",
"$\\frac{2\\sqrt{3} - 3}{3}$",
"$7\\sqrt{3} - 12$",
"$3\\sqrt{3} - 5$",
"$\\frac{9 - 5\\sqrt{3}}{3}$"
] | images/2338.jpg | C | null | 5 | metric geometry - area |
|
46 | What do you see if you look at the tower, which is made up of two building blocks, exactly from above?
<image1>
<image2> | [
"A",
"B",
"C",
"D",
"E"
] | images/46.jpg | A | null | 2 | descriptive geometry |
|
2620 | Consider these two geoboard quadrilaterals. Which of the following statements is true?
<image1> | [
"$\\text{The area of quadrilateral I is more than the area of quadrilateral II.}$",
"$\\text{The area of quadrilateral I is less than the area of quadrilateral II.}$",
"$\\text{The quadrilaterals have the same area and the same perimeter.}$",
"$\\text{The quadrilaterals have the same area, but the perimeter of I is more than the perimeter of II.}$",
"$\\text{The quadrilaterals have the same area, but the perimeter of I is less than the perimeter of II.}$"
] | images/2620.jpg | E | null | 4 | combinatorial geometry |
|
1313 | Rectangle $A B C D$ intersects the circle at points $E, F$, $G, H$. If $A E=4 \mathrm{~cm}, E F=5 \mathrm{~cm}, D H=3 \mathrm{~cm}$, then the length of $H B$ is
<image1> | [
"$6 \\mathrm{~cm}$",
"$7 \\mathrm{~cm}$",
"$\\frac{20}{3} \\mathrm{~cm}$",
"$8 \\mathrm{~cm}$",
"$9 \\mathrm{~cm}$"
] | images/1313.jpg | B | null | 4 | metric geometry - length |
|
178 | Five cards are lying on the table in the order 1,3,5,4,2. You must get the cards in the order $1,2,3,4,5$. Per move, any two cards may be interchanged. How many moves do you need at least?
<image1> | [] | images/178.jpg | 2 | null | 5 | algebra |
|
669 | Aladdin's carpet has the shape of a square. Along each edge there are two rows of dots (see diagram). The number of points is the same along each edge. How many dots in total does the carpet have?
<image1> | [] | images/669.jpg | 32 | null | 3 | arithmetic |
|
2078 | Cube $ABCDEFGH$, labeled as shown below, has edge length $1$ and is cut by a plane passing through vertex $D$ and the midpoints $M$ and $N$ of $\overline{AB}$ and $\overline{CG}$ respectively. The plane divides the cube into two solids. The volume of the larger of the two solids can be written in the form $\frac{p}{q}$, where $p$ and $q$ are relatively prime positive integers. Find $p+q$.
<image1> | [] | images/2078.jpg | 89 | null | 3 | solid geometry |
|
1775 | The diagram shows three triangles which are formed by the five line segments $A C D F, B C G, G D E, A B$ and $E F$ so that $A C=B C=C D=G D=D F=E F$. Also $\angle C A B=\angle E F D$. What is the size, in degrees, of $\angle C A B$ ? <image1> | [] | images/1775.jpg | 60 | Let the size in degrees of $\angle C A B$ be $x$. Since $A C=B C$, triangle $A B C$ is isosceles. Hence $\angle A B C=x^{\circ}$. Since angles in a triangle add to $180^{\circ}$, we have $\angle B C A=(180-2 x)^{\circ}$. Also, since vertically opposite angles are equal, we have $\angle G C D=(180-2 x)^{\circ}$. The same argument can then be applied to triangle $C G D$ which is isosceles since $C D=G D$. Hence $\angle C D G=(180-2(180-2 x))^{\circ}=(4 x-180)^{\circ}$. Therefore, since vertically opposite angles are equal, $\angle F D E=(4 x-180)^{\circ}$. The same argument can be applied once more, this time to triangle $F D E$, which is also isosceles since $D F=E F$. This gives $\angle E F D=(180-2(4 x-180))^{\circ}=(540-8 x)^{\circ}$. However, we are also told that $\angle C A B=\angle E F D$ and hence $x=540-8 x$ or $9 x=540$. This has solution $x=60$ and hence the size, in degrees, of $\angle C A B$ is 60 . | 3 | metric geometry - angle |
|
848 | A rectangle is formed from 4 equally sized smaller rectangles. The shorter side is $10 \mathrm{~cm}$ long. How long is the longer side?
<image1> | [
"$40 \\mathrm{~cm}$",
"$30 \\mathrm{~cm}$",
"$20 \\mathrm{~cm}$",
"$10 \\mathrm{~cm}$",
"$5 \\mathrm{~cm}$"
] | images/848.jpg | C | null | 2 | combinatorial geometry |
|
159 | The two markers with a question mark have the same number.
<image1>
Which number do you have to put instead of the question mark so that the calculation is correct? | [] | images/159.jpg | 3 | null | 1 | algebra |
|
382 | Emma should colour in the three strips of the flag shown. She has four colours available. She can only use one colour for each strip and immediately adjacent strips are not to be of the same colour. How many different ways are there for her to colour in the flag? <image1> | [] | images/382.jpg | 36 | null | 5 | graph theory |
|
2110 | Figures $ 0$, $ 1$, $ 2$, and $ 3$ consist of $ 1$, $ 5$, $ 13$, and $ 25$ nonoverlapping squares, respectively. If the pattern were continued, how many nonoverlapping squares would there be in figure $ 100$?
<image1> | [] | images/2110.jpg | 20201 | null | 3 | algebra |
|
368 | The points $A, B, C$ and $D$ are marked on a straight line in this order as shown in the diagram. We know that $A$ is $12 \mathrm{~cm}$ from $C$ and that $B$ is $18 \mathrm{~cm}$ from $D$. How far apart from each other are the midpoints of the line segments $A B$ and $C D$?
<image1> | [
"$6 \\mathrm{~cm}$",
"$9 \\mathrm{~cm}$",
"$12 \\mathrm{~cm}$",
"$13 \\mathrm{~cm}$",
"$15 \\mathrm{~cm}$"
] | images/368.jpg | E | null | 5 | metric geometry - length |
|
2888 | In the diagram, if $\triangle ABC$ and $\triangle PQR$ are equilateral, then what is the measure of $\angle CXY$ in degrees? <image1> | [] | images/2888.jpg | 40 | Since $\triangle ABC$ and $\triangle PQR$ are equilateral, then $\angle ABC=\angle ACB=\angle RPQ=60^\circ$.
Therefore, $\angle YBP = 180^\circ-65^\circ-60^\circ=55^\circ$ and $\angle YPB = 180^\circ-75^\circ-60^\circ=45^\circ$.
In $\triangle BYP$, we have $\angle BYP = 180^\circ - \angle YBP - \angle YPB = 180^\circ - 55^\circ-45^\circ=80^\circ$.
Since $\angle XYC = \angle BYP$, then $\angle XYC=80^\circ$.
In $\triangle CXY$, we have $\angle CXY = 180^\circ - 60^\circ - 80^\circ = 40^\circ$.
So our final answer is $\boxed{40}$ degrees. | 1 | metric geometry - angle |
|
2934 | In isosceles triangle $ABC$, if $BC$ is extended to a point $X$ such that $AC = CX$, what is the number of degrees in the measure of angle $AXC$? <image1> | [] | images/2934.jpg | 15 | The angles opposite the equal sides of $\triangle ABC$ are congruent, so $\angle BCA=30^\circ$. Since $\angle BCA$ and $\angle XCA$ are supplementary, we have \begin{align*}
\angle XCA &= 180^\circ - \angle BCA\\
&= (180-30)^\circ \\
&= 150^\circ.
\end{align*} Since $\triangle ACX$ is isosceles with $AC=CX$, the angles $\angle XAC$ and $\angle AXC$ are congruent. Let each of them be $x^\circ$. Then the sum of angles in $\triangle ACX$ is $180^\circ$, so $$x + x + 150 = 180,$$ yielding $x=15$. That is, $\angle AXC = \boxed{15}$ degrees. | 1 | metric geometry - angle |
|
1773 | Andrew wants to write the letters of the word KANGAROO in the cells of a $2 \times 4$ grid such that each cell contains exactly one letter. He can write the first letter in any cell he chooses but each subsequent letter can only be written in a cell with at least one common vertex with the cell in which the previous letter was written. Which of the following arrangements of letters could he not produce in this way?
<image1> | [
"A",
"B",
"C",
"D",
"E"
] | images/1773.jpg | D | To produce the arrangement of diagram D, Andrew would first need to write the letters K, A, N and $\mathrm{G}$ in the top four cells as shown. He would then need to write $\mathrm{A}$ in a vacant cell next to the G. Therefore he could not write $\mathrm{O}$ and $\mathrm{O}$ in the third row. Hence arrangement D could not be produced in the way described. (It is left as an exercise for readers to show that all the other arrangements can be produced in the way described.) | 3 | combinatorics |
|
1688 | Costa is building a new fence in his garden. He uses 25 planks of wood, each of which is $30 \mathrm{~cm}$ long. He arranges these planks so that there is the same slight overlap between any two adjacent planks, as shown in the diagram. The total length of Costa's new fence is 6.9 metres. What is the length in centimetres of the overlap between any pair of adjacent planks? <image1> | [] | images/1688.jpg | 2.5 | Let the length of the overlap be $y \mathrm{~cm}$. From the diagram in the question, it can be seen that the total length of the fence can be calculated as the total length of the 13 pieces in the lower row in the diagram and the total length of the 12 planks in the upper row of the diagram, with each of the 12 having two overlaps removed. Hence $690=13 \times 30+12 \times(30-2 y)$. Therefore $690=390+360-24 y$ and hence $24 y=60$. This has solution $y=2.5$. Therefore the overlap between adjacent planks is $2.5 \mathrm{~cm}$. | 2 | metric geometry - length |
|
975 | A building is made up of cubes of the same size. The three pictures show it from above (von oben), from the front (von vorne) and from the right (von rechts). What is the maximum number of cubes used to make this building?
<image1> | [] | images/975.jpg | 19 | null | 5 | descriptive geometry |
|
2281 | In this figure $\angle RFS = \angle FDR$, $FD = 4$ inches, $DR = 6$ inches, $FR = 5$ inches, $FS = 7\frac{1}{2}$ inches. The length of $RS$, in inches, is:
<image1> | [
"$\\text{undetermined}$",
"$4$",
"$5\\frac{1}{2}$",
"$6$",
"$6\\frac{1}{4}$"
] | images/2281.jpg | E | null | 5 | metric geometry - length |
|
898 | The figure shown on the right consists of one square part and eight rectangular parts. Each part is $8 \mathrm{~cm}$ wide. Peter assembles all parts to form one long, $8 \mathrm{~cm}$ wide rectangle. How long is this rectangle?
<image1> | [
"$150 \\mathrm{~cm}$",
"$168 \\mathrm{~cm}$",
"$196 \\mathrm{~cm}$",
"$200 \\mathrm{~cm}$",
"$232 \\mathrm{~cm}$"
] | images/898.jpg | D | null | 2 | combinatorial geometry |
|
2800 | Let $A_1 = (0, 0)$, $B_1 = (1, 0)$, $C_1 = (1, 1)$, $D_1 = (0, 1)$. For all $i > 1$, we recursively define\n$$A_i =\frac{1}{2020} (A_{i-1} + 2019B_{i-1}),B_i =\frac{1}{2020} (B_{i-1} + 2019C_{i-1})$$$$C_i =\frac{1}{2020} (C_{i-1} + 2019D_{i-1}), D_i =\frac{1}{2020} (D_{i-1} + 2019A_{i-1})$$where all operations are done coordinate-wise.\n\nIf $[A_iB_iC_iD_i]$ denotes the area of $A_iB_iC_iD_i$, there are positive integers $a, b$, and $c$ such that $\sum_{i=1}^{\infty}[A_iB_iC_iD_i] = \frac{a^2b}{c}$, where $b$ is square-free and $c$ is as small as possible. Compute the value of $a + b + c$\n<image1> | [] | images/2800.jpg | 3031 | Solution: We note that by symmetry, there is a $k$ such that $\left[A_i B_i C_i D_i\right]=k\left[A_{i-1} B_{i-1} C_{i-1} D_{i-1}\right]$ for all $i$. We can see that $1=\left[A_1 B_1 C_1 D_1\right]=\left[A_2 B_2 C_2 D_2\right]+4\left[A_1 A_2 D_2\right]=\left[A_2 B_2 C_2 D_2\right]+\frac{4038}{2020^2}$, hence $k=1-\frac{2019}{2 \cdot 1010^2}$. Using the geometric series formula, we get\n$$\n\sum_{i=1}^{\infty}\left[A_i B_i C_i D_i\right]=\frac{1}{1-k}=\frac{1010^2 \cdot 2}{2019} \Longrightarrow 3031 .\n$$ | 5 | metric geometry - area |
|
1173 | Lisas aviation club designs a flag with a flying "dove" on a $4 \times 6$-grid. The area of the "dove" is $192 \mathrm{~cm}^{2}$. The perimeter of the "dove" is made up of straight lines and circular arcs. What measurements does the flag have?
<image1> | [
"$6 \\mathrm{~cm} \\times 4 \\mathrm{~cm}$",
"$12 \\mathrm{~cm} \\times 8 \\mathrm{~cm}$",
"$20 \\mathrm{~cm} \\times 12 \\mathrm{~cm}$",
"$24 \\mathrm{~cm} \\times 16 \\mathrm{~cm}$",
"$30 \\mathrm{~cm} \\times 20 \\mathrm{~cm}$"
] | images/1173.jpg | D | null | 4 | combinatorial geometry |
|
3013 | What is the volume of a pyramid whose base is one face of a cube of side length $2$, and whose apex is the center of the cube? Give your answer in simplest form.
<image1> | [] | images/3013.jpg | \frac{4}{3} | The base of the pyramid is a square of side length $2$, and thus has area $2^2=4$. The height of the pyramid is half the height of the cube, or $\frac{1}{2}\cdot 2 = 1$. Therefore, the volume of the pyramid is \begin{align*}
\frac{1}{3}\cdot (\text{area of base})\cdot (\text{height}) &= \frac{1}{3}\cdot 4\cdot 1 \\
&= \boxed{\frac{4}{3}}.
\end{align*} | 1 | solid geometry |
|
2930 | In $\triangle ABC$, what is the value of $x + y$? <image1> | [] | images/2930.jpg | 90 | Since $\triangle BDA$ is isosceles, $\angle BAD = \angle ABD = x^\circ$.
Since $\triangle CDA$ is isosceles, $\angle CAD = \angle ACD = y^\circ$. [asy]
import olympiad;
size(7cm);
pair a = dir(76);
pair b = (-1, 0);
pair c = (1, 0);
pair o = (0, 0);
draw(a--b--c--cycle);
draw(a--o);
label("$A$", a, N); label("$B$", b, SW); label("$C$", c, SE); label("$D$", o, S);
label("$104^\circ$", o, 1.8 * NW + 0.4 * E);
label("$x^\circ$", b, 3 * E + NE + NE);
label("$y^\circ$", c, 2 * W + 2 * NW);
add(pathticks(b--o, s=3));
add(pathticks(c--o, s=3));
add(pathticks(a--o, s=3));
label("$x^\circ$", a, 3 * S + 2 * SW + W); label("$y^\circ$", a, 3 * S + SE);
[/asy] Therefore, $\angle BAC = (x + y)^\circ$.
Since the sum of the angles in $\triangle ABC$ is $180^\circ$, we have \begin{align*}
x + y + (x + y) &= 180\\
2x + 2y &= 180\\
x + y &= 90.
\end{align*}Therefore, $x + y = \boxed{90}$. | 1 | metric geometry - angle |
|
1453 | Six rectangles are arranged as shown. The top left-hand rectangle has height $6 \mathrm{~cm}$. The numbers within the rectangles indicate their areas in $\mathrm{cm}^{2}$. What is the height of the bottom right-hand rectangle?
<image1> | [
"$4 \\mathrm{~cm}$",
"$5 \\mathrm{~cm}$",
"$6 \\mathrm{~cm}$",
"$7.5 \\mathrm{~cm}$",
"$10 \\mathrm{~cm}$"
] | images/1453.jpg | B | null | 4 | metric geometry - length |
End of preview. Expand
in Data Studio
README.md exists but content is empty.
- Downloads last month
- 121